Essenzen des Selbermachens – Technik, Software & Wissenschaft

Gleitende Mittelwerte

Der gleitende Durchschnitt ist eine mathematische Methode zur Glättung eines gegebenen Datenverlaufes. Die Idee hinter der Methode basiert darauf, kurzfristige Schwankungen zu reduzieren und dafür langfristige Trends deutlicher sichtbar werden zu lassen.

Basierend auf „Moving Average"-Systemen wurden eine Vielzahl von Methoden abgeleitet, von denen heute vor allem drei bedeutend sind: „simple" (einfache), „weighted" (gewichtete), „exponential" (exponentielle). Darüber hinaus gibt es noch weitere wie „triangular" sowie „variable" „Moving Averages", die sich jeweils durch die Gewichtung der Daten unterscheiden.Auf die aber hier nicht weiter eingegangen werden soll.

Typ	Beschreibung	Formel (LaTeX)
Einfacher gleitender Mittelwert (SMA)	Durchschnitt der letzten n Werte	\( SMA_t = \frac{1}{n} \sum_{i=0}^{n-1} x_{t-i} \)
Gewichteter gleitender Mittelwert (WMA)	Jüngere Werte erhalten ein höheres Gewicht	\( WMA_t = \frac{\sum w_i x_{t-i}}{\sum w_i} \)
Exponentiell gleitender Mittelwert (EMA)	Exponentiell abnehmende Gewichtung	\( EMA_t = \alpha x_t + (1 - \alpha) EMA_{t-1} \)

Die Glättung erfolgt durch das Abschwächen von besonders hohen Werten. Dies geschieht, indem eine neue Datenreihe erstellt wird, die aus den Durchschnitten von gleich großen Datenmengen berechnet werden. Dabei werden die Datenpunkte der Reihe durch den arithmetischen Mittelwert der Nachbarpunkte (oder einer gewichteten Form davon) ersetzt. Im einfachsten Fall geschieht dies durch Mittelung von drei Datenpunkten (der ausgewählte Datenpunkt und seine beiden Nachbarn). Man spricht in diesem Zusammenhang auch von einem Fenster. Die Fenstergröße ist ein zentraler Parameter bei der Berechnung von gleitenden Mittelwerten:

Kleine Fenstergrößen (z.B. 3–5): Reagiert schnell, aber anfällig für Rauschen
Mittel (z.B. 10–20): Gute Balance zwischen Glättung und Reaktionsfähigkeit
Groß (z.B. 50–200): Filtert kurzfristige Schwankungen heraus, Ideal für langfristige Trends, z. B. in der Börsenanalyse

Zusammenfassend kann man festhalten: Je größer das Fenster, desto stärker die zeitliche Verzögerung. Der Durchschnitt „hinkt dabei hinterher“, weil er viele vergangene Werte einbezieht. Kleine Fenster erkennen Trendwechsel schneller und zeigen höhere Volatilität im Durchschnitt. Große Fenster wirken dagegen beruhigend und stabilisieren die Darstellung.

Einfaches Beispiel

Ausgehend von einer kurzen zufälligen Liste mit Daten:


    RandomInteger[{1, 10}, 20]
    {7, 5, 4, 2, 2, 5, 9, 10, 5, 10, 2, 7, 2, 6, 8, 9, 7, 9, 1, 6}

    /* Ausgehend von dieser Zahlenreihe würde man durch */
    /* eine Fenstergröße von n=3 folgende neue Datenreihe erzeugen:  */
    {7,(7+5+4)/3, 4,... }
    {7,5.33, 4, 2,...}
    {7,5.33,(5.33+4+2)/3,2}
    {7,5.33, 3.55, 2,...}

Positionierung des Mittelwerts in der Datenliste

Die Positionierung des gleitenden Mittelwerts innerhalb der Datenreihe beeinflusst maßgeblich, wie man Trends und Muster interpretiert. Es gibt drei gängige Methoden zur Einordnung des Mittelwerts (des Wertes der innerhalb des Fensters berechnet wird) in die Datenliste:

Typ	Beschreibung	Position des Mittelwerts im Fenster
Nachlaufender Mittelwert (Trailing)	Der Mittelwert wird dem letzten Wert des betrachteten Fensters zugeordnet.	Ende (rechts)
Vorlaufender Mittelwert (Leading)	Der Mittelwert wird dem ersten Wert des Fensters zugeordnet.	Anfang (links)
Zentrierter Mittelwert (Centered)	Der Mittelwert wird dem mittleren Wert des Fensters zugeordnet.	Mitte


		Angenommen wir haben folgende Datenliste:
		[10, 12, 14, 16, 18]  –> Mittelwert 70/5 = 14
		Fenstergröße: 5
		Nachlaufend: MA wird bei Position 5 (Wert 18) eingesetzt
		Vorlaufend : MA wird bei Position 1 (Wert 10) eingesetzt
		Zentriert  : MA wird bei Position 3 (Wert 14) eingesetzt

		Trailing ist Standard in Finanzanalyse, weil man nur vergangene Daten nutzt.
		Centered ist beliebt in der Signalverarbeitung oder bei historischen Analysen.
		Leading ist experimentell und wird selten verwendet, da es auf zukünftige Daten zugreift.

Mit Mathematica kann man sich die unterschiedlichen Auswirkungen der Positionierung sehr schön veranschaulichen:


		    ClearAll[MovingAveragePositioniert]
		    MovingAveragePositioniert[daten_List, fenster_Integer] :=
			Module[{n, shift, maTrailingRaw, maCenteredRaw, maLeadingRaw,
			  maTrailing, maCentered, maLeading, mittelwerte},
			 n = Length[daten];
			 shift = Floor[fenster/2];
			 (*Trailing MA*)maTrailingRaw = MovingAverage[daten, fenster];
			 maTrailing = PadLeft[maTrailingRaw, n];
			 (*Centered MA*)
			 maCenteredRaw =
			  Table[Mean[daten[[i ;; i + fenster - 1]]], {i, 1, n - fenster + 1}];
			 maCentered = PadLeft[PadRight[maCenteredRaw, n - shift], n];
			 (*Leading MA*)
			 maLeadingRaw =
			  Table[Mean[daten[[i ;; i + fenster - 1]]], {i, 1, n - fenster + 1}];
			 maLeading = PadRight[maLeadingRaw, n];
			 (*Gesamtdurchschnitte*)
			 mittelwerte = {Mean[daten],
			   Mean[DeleteCases[maLeading, _Missing | Null]],
			   Mean[DeleteCases[maCentered, _Missing | Null]],
			   Mean[DeleteCases[maTrailing, _Missing | Null]]};
			 (*Ausgabe*)
			 Column[{Style["Gleitende Mittelwerte (Positioniert)", Bold],
			   TableForm[Transpose[{daten, maLeading, maCentered, maTrailing}],
			    TableHeadings -> {None, {"Original", "Leading MA", "Centered MA",
				   "Trailing MA"}}], Style["Gesamtdurchschnitte:", Bold],
			   Grid[{{"Originaldaten", mittelwerte[[1]]}, {"Leading MA",
				 mittelwerte[[2]]}, {"Centered MA",
				 mittelwerte[[3]]}, {"Trailing MA", mittelwerte[[4]]}},
			    Frame -> All]}]]

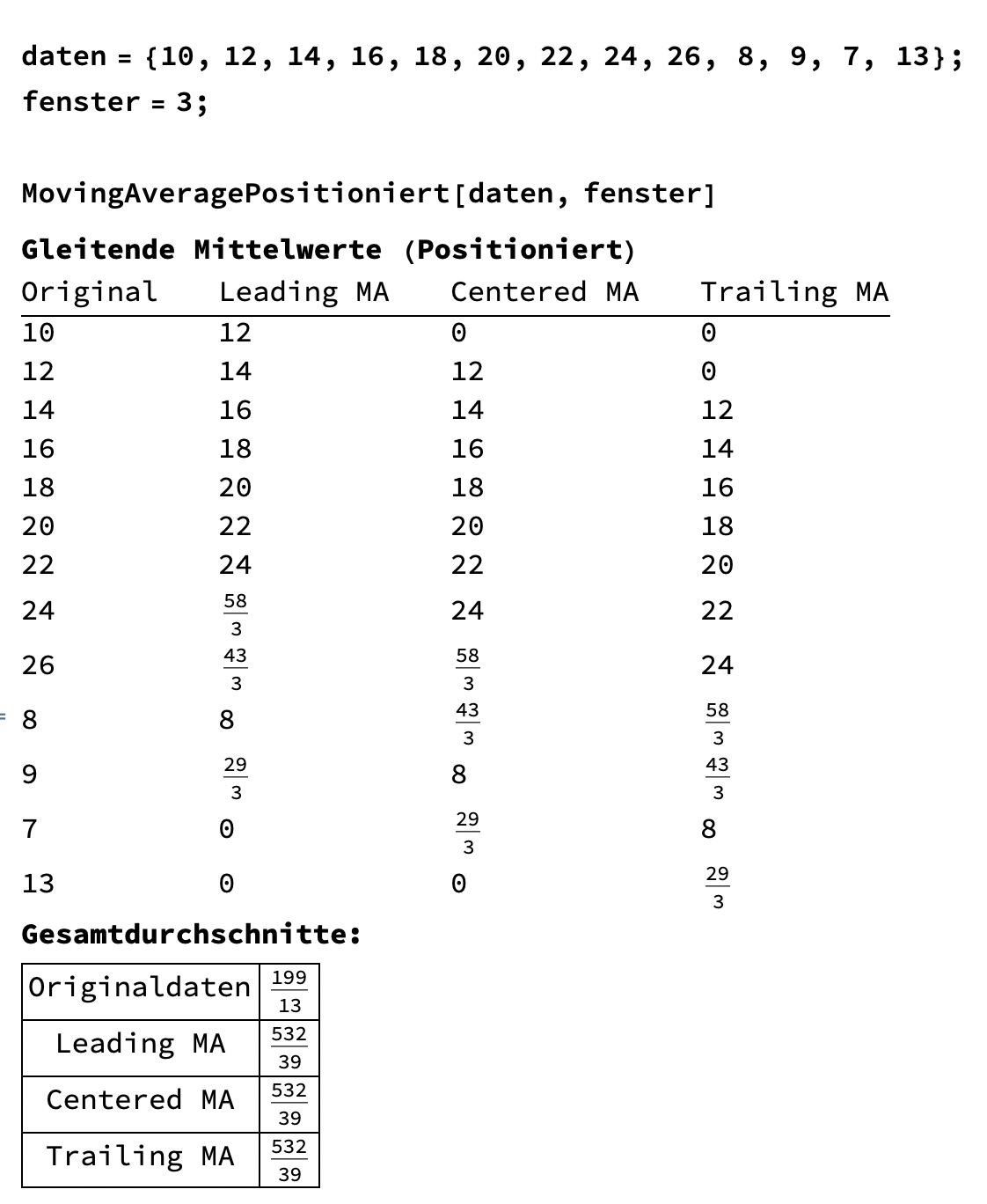
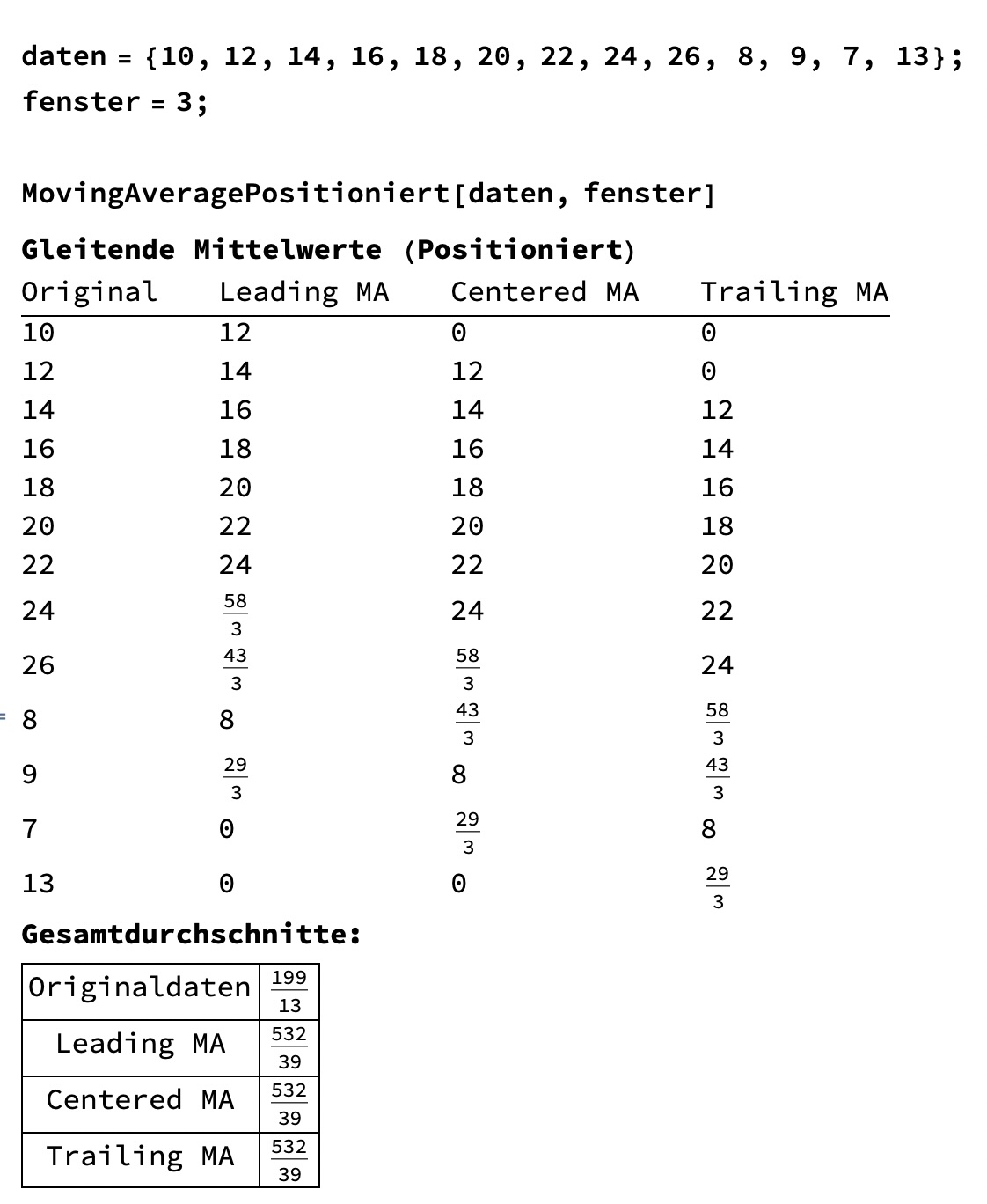
Mathematica Ergebnis: Vergleich der drei Moving-Average-Varianten jeweils mit Fenstergröße 3

Der etwas umfngreiche Mathematica Code dient nur zur Veranschaulichung der unterschiedlichen Positionierungs-Methoden. Ich denke es ist schon den AUfwand Wert, um zu verstehen welchen Einfluß die Positionierung der gleitenden Mittelwerte sowie die Größe des Fensters haben:
Orginaldaten liefern einen Mittelwert von: 199/13=15.3 mit der Trailing Positionierung erhalten wir: 13.64. Schon ein beachtenswerter Unterschied. Vergrößert man zusätzlich das Fenster auf 4 erhält man Trailing MAs von: 12.42, mit Fenster 5: 11.93
Für die meisten Anwendung in der Praxis kann man sich den ganzen Aufwand ersparen, und die eingebaute Mathematica Funktion MovingAverage[list,window] verwenden, die mit der Trailing-Positionierung arbeitet. Mit den Daten des obigen Beispiels würde folgendes Ergebnis entstehen:


		daten = {10, 12, 14, 16, 18, 20, 22, 24, 26, 8, 9, 7, 13};
		MovingAverage[daten, 3]

		=> {12, 14, 16, 18, 20, 22, 24, 58/3, 43/3, 8, 29/3}

Umsetzung in Python

Neben Mathematica (das sich natürlich ideal für derartige Aufgaben eignet) kann man auch Python einsetzen. Ein einfaches Programm, das ebenfalls die Trailing-Positionierung verwendet, könnte so aussehen:


		  def moving_average_trailing(data, window):
			 if window < 1:
				raise ValueError("Fenstergröße muss mindestens 1 sein.")
			 result = []
			 for i in range(window - 1, len(data)):
				avg = sum(data[i - window + 1:i + 1]) / window
				result.append(avg)
			 return result

		  # Beispiel-Daten
		  daten = [10, 12, 14, 16, 18, 20, 22, 24, 26, 8, 9, 7, 13]
		  fenster = 3

		  # Berechnung
		  ma_trailing = moving_average_trailing(daten, fenster)

		  # Ausgabe
		  print("Trailing Moving Average (Fenstergröße 3):")
		  print(ma_trailing)

		  =>Trailing Moving Average (Fenstergröße 3):
		  [12.0, 14.0, 16.0, 18.0, 20.0, 22.0, 24.0, 19.333333333333332, 14.333333333333334,
		  8.0, 9.666666666666666]

Es gibt verschiedenste Möglichkeiten, wo diese Methode angewendnet werden. Beispielsweise bei der Glättung von Sensordaten. Wie das mit einem Arduino realisiert werden kann, findet sich sehr anschaulich auf der Seite Shelvin dargestellt.

⬅ Zurück zur Hauptseite